OpenGL中的光照

颜色

我们都知道人的眼睛之所以能够看到东西, 有两种情况:

我们看到了这个物体发出的光线
这个物体反射了一个发光物体发出的光线

而每个物体都有不同的颜色, 这是因为他们对光线有不同的反射能力, 比如太阳下树叶反射了太阳发出的白色光中的绿色, 人眼接收到了这个光线从而认为树叶是绿色的. 如果将树叶放置在红色灯光下, 树叶会吸收除了绿色光之外的所有光线, 从而显现出黑色.

一个物体对某种颜色的反射能力我们成为反射率

如果我们使用一个三维向量来描述光的颜色, 那么经过反射之后物体的颜色的某一个分量就等于光源的这个分量乘以物体对该颜色分量的反射率.

基础光照

显示中的光照是极其复杂的，而且会受到诸多因素的影响，这是我们有限的计算能力所无法模拟的。

因此OpenGL的光照使用的是简化的模型，对现实的情况进行近似，这样处理起来会更容易一些，而且看起来也差不多一样。这些光照模型都是基于我们对光的物理特性的理解。其中一个模型被称为风氏光照模型(Phong Lighting Model)。

风氏光照主要有以下三个部分:

环境光(Ambient)
漫反射(Diffuse)
镜面光(Specular)

材质

在现实世界里，每个物体会对光产生不同的反应。比如，钢制物体看起来通常会比陶土花瓶更闪闪发光，一个木头箱子也不会与一个钢制箱子反射同样程度的光。有些物体反射光的时候不会有太多的散射(Scatter)，因而产生较小的高光点，而有些物体则会散射很多，产生一个有着更大半径的高光点。如果我们想要在OpenGL中模拟多种类型的物体，我们必须针对每种表面定义不同的材质(Material)属性。

下面的代码中我们通过设置漫反射贴图和镜面光贴图来定义一种材质.

struct Material {
    sampler2D diffuse;
    sampler2D specular;    
    float shininess;
};

通过使用漫反射和镜面光贴图，我们可以给相对简单的物体添加大量的细节。我们甚至可以使用法线/凹凸贴图(Normal/Bump Map)或者反射贴图(Reflection Map)给物体添加更多的细节.

投光物

平行光

当一个光源处于很远的地方时，来自光源的每条光线就会近似于互相平行。不论物体和/或者观察者的位置，看起来好像所有的光都来自于同一个方向。当我们使用一个假设光源处于无限远处的模型时，它就被称为定向光，因为它的所有光线都有着相同的方向，它与光源的位置是没有关系的。

定向光非常好的一个例子就是太阳。太阳距离我们并不是无限远，但它已经远到在光照计算中可以把它视为无限远了。所以来自太阳的所有光线将被模拟为平行光线.

点光源

定向光对于照亮整个场景的全局光源是非常棒的，但除了定向光之外我们也需要一些分散在场景中的点光源(Point Light)。点光源是处于世界中某一个位置的光源，它会朝着所有方向发光，但光线会随着距离逐渐衰减。想象作为投光物的灯泡和火把，它们都是点光源。

光线衰减

随着光线传播距离的增长逐渐削减光的强度通常叫做衰减(Attenuation)。随距离减少光强度的一种方式是使用一个线性方程。这样的方程能够随着距离的增长线性地减少光的强度，从而让远处的物体更暗。然而，这样的线性方程通常会看起来比较假。在现实世界中，灯在近处通常会非常亮，但随着距离的增加光源的亮度一开始会下降非常快，但在远处时剩余的光强度就会下降的非常缓慢了。所以，我们需要一个不同的公式来减少光的强度。

F_{att}=\frac{1.0}{K_c+K_l*d+K_q*d^2}

其中常数项 $K_c$ , 一次项 $K_l$ , 二次项 $K_q$ 是我们可以自定义的.

常数项通常保持为1.0，它的主要作用是保证分母永远不会比1小，否则的话在某些距离上它反而会增加强度，这肯定不是我们想要的效果.
一次项会与距离值相乘，以线性的方式减少强度。
二次项会与距离的平方相乘，让光源以二次递减的方式减少强度。二次项在距离比较小的时候影响会比一次项小很多，但当距离值比较大的时候它就会比一次项更大了

聚光

聚光(Spotlight)是位于环境中某个位置的光源，它只朝一个特定方向而不是所有方向照射光线。这样的结果就是只有在聚光方向的特定半径内的物体才会被照亮，其它的物体都会保持黑暗。聚光很好的例子就是路灯或手电筒。

OpenGL中聚光是用一个世界空间位置、一个方向和一个切光角(Cutoff Angle)来表示的，切光角指定了聚光的半径（译注：是圆锥的半径不是距光源距离那个半径）。对于每个片段，我们会计算片段是否位于聚光的切光方向之间（也就是在锥形内），如果是的话，我们就会相应地照亮片段。

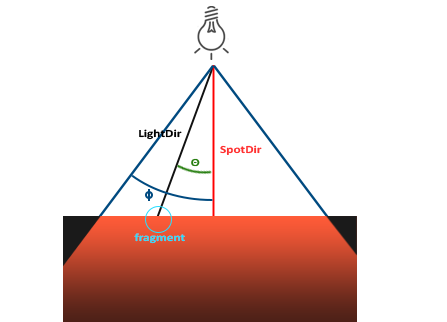
spotlight demo

LightDir: 从片段指向光源的向量
SpotDir: 聚光指向的方向
$\phi$ : 指定了聚光半径的切光角。落在这个角度之外的物体都不会被这个聚光所照亮
$\theta$ : LightDir向量和SpotDir向量之间的夹角。在聚光内部的 $\theta$ 值应该比 $\phi$ 值小

平滑边缘

我们可以通过定义内外两个切光角, 在这两个切光角之间进行渐变来实现软化边缘的效果, 我们可以用这个公式来计算这个值:

I=\frac{\theta-\gamma}{\epsilon}

这里 $\epsilon$ (Epsilon)是内（ $\phi$ ）和外圆锥（ $\gamma$ ）之间的余弦值差（ $\epsilon=\phi-\gamma$ ）。最终的 $I$ 值就是在当前片段聚光的强度。

我们来解释以下这个函数是怎么运行的, 因为我们内切和外切角需要位于 $(0,\frac{\pi}{2})$ 之间, 在这个范围内余弦函数是单调递减的. 因为内切角 $\phi$ 和外切角 $\gamma$ 不变, 所以当入射角 $\theta$ 从垂直平面移动到水平与平面也就是从0到 $\frac{\pi}{2}$ 的过程中, $cos(\theta)$ 是单调递减的, 这个值在 $\theta=0$ 的时候最大, 在 $\theta>\phi$ 的时候开始小于1, 在 $\theta=\gamma$ 的时候等于0, 大于 $\gamma$ 的时候为负数. 如果我们使用截断函数将函数值限制在 $[0,1]$ 区间内, 就可以表示出内切角以内全亮, 外切角以外全暗, 两个切角之间光线平滑减弱的效果.

法线矩阵

一个片段在进行model变换的时候, 它的法线是如何变化的呢? 如果这个片段进行的是正常的旋转或者位移变换, 那么法线只需要进行同样的操作即可. 同时, 如果这个片段进行了均匀缩放(每个分量上的缩放程度相同), 那么法线也只需要进行相同的操作.

但是, 这个里有一个特例, 那就是当片段进行非均匀缩放的时候, 法线不可以简单的进行相同的操作, 下面的这张图可以直观的解释为什么不能:

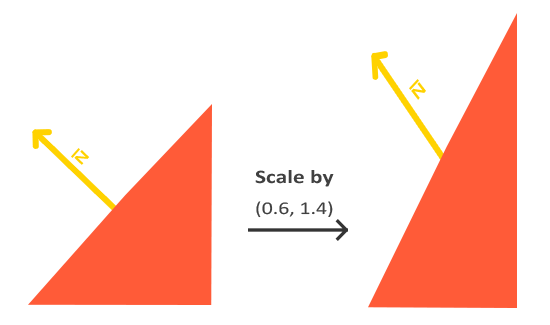normal demo 很明显第二个法线不再垂直于平面了, 我们可以通过法线矩阵来解决这个问题.

法线矩阵是model矩阵的逆转置矩阵. 即 $M_n=(M^{-1})^T$ .

为什么是逆转置矩阵

假设我们需要一个变换矩阵 $A$ 来将原先的法向量 $n$ 来变换为垂直于变换后的片段的向量 $n^{'}$ , 假设片段在这一点的切线为 $t$ , 那么 $n\cdot t=0$ . 变换之后的切线为 $Mt$ , 那么就需要 $n^{'}\cdot (Mt)=0$ .

那么 $(An)\cdot (Mt)=0$ .

使用点积计算结果, 得到

n^TA^TMt=0

又因为初始条件 $n^Tt=0$ 对所有切线t成立, 所以 $A^TM=I$ , 其中I是单位矩阵.

则可以解出:

A^T=M^{-1} \rightarrow A=(M^{-1})^T

所以, 法线矩阵必须是model矩阵的逆转置矩阵. 矩阵的逆转置求解是一个昂贵的操作, 所以只有在片段进行了非均匀缩放, 并且M不是正交矩阵( $M^{-1}\neq M^T$ )的情况下才进行计算.